[Home] [GRP] [RES] [PUB] [ETC] [LEC] [S/W]
 

Software and Downloads

Please check out our GitHub repository. New code will be released on GitHub. Most of the downloads found on this page have migrated to GitHub and might not get updated here.

Contents

Plotting Atomic Orbitals (AOs) with Mathematica

Plotting Molecular Orbitals (MOs) with Mathematica

Plotting rank-2 tensors

Manipulate CUBE format volume data files

Crystal field Hamiltonian and atomic shell splitting

PNMRShift: A software tool for NMR shifts of paramagnetic molecules

KK-GUI: Software with graphical interface to perform Kramers-Kronig transformations

CD spectra toolkit

Template for plots of spectra (or other stuff) with Gnuplot and LaTeX

______________________

Plotting Atomic Orbitals (AOs) with Mathematica

(explore on GitHub)
 
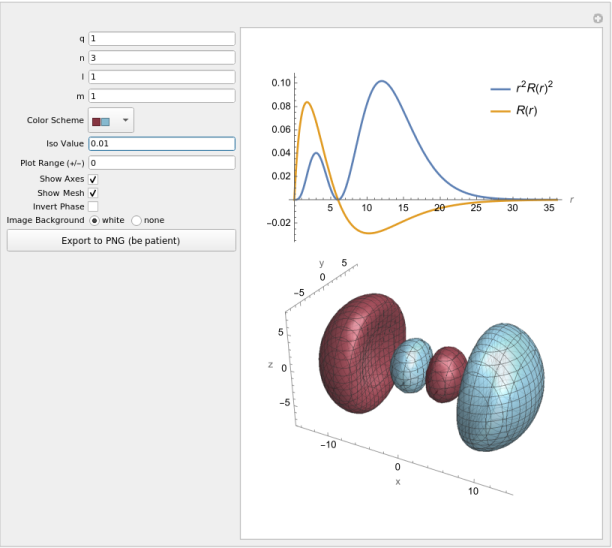
Screenshot of a graphical interface for plotting atomic orbitals: radial density in blue and radial function in orange above a 3D isosurface representation of an atomic orbital in red and blue lobes. Input fields (quantum numbers n, l, m, etc.), toggles, and an ’Export to PNG (be patient)’ label appear at left.
You can use this notebook to visualize the orbitals (wavefunctions) of hydrogen-like atoms. The plot interface is shown above, along with visualizations of a 3px hydrogen orbital. For non-zero values of the magnetic quantum number m, the usual real ’sine’ and ’cosine’ linear combinations are created for -/+m.

______________________

Plotting Molecular Orbitals (MOs) with Mathematica

(explore on GitHub)
 
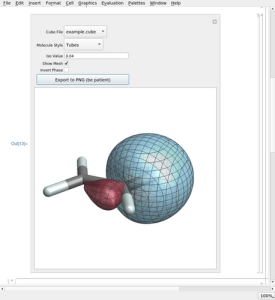
Graphical interface showing a 3D molecular orbital visualization: a central molecule with a large transparent blue spherical lobe and a smaller red lobe representing the orbital as isosurfaces. The molecule is displayed in ’Tubes’ style, with hydrogen and carbon atoms shown as cylinders. Controls at the top allow selection of a cube file, isovalue, and options to show mesh or invert phase. A button labeled ’Export to PNG (be patient)’ appears below the controls. 3D molecular orbital visualization: a central molecule with several purple and green lobes representing the orbital as isosurfaces. The molecule is displayed in ’Tubes’ style, with hydrogen, carbon, and nitrogen atoms shown in off white, gray, and blue, respectively.
Rather: Plotting isosurfaces of molecular orbitals... Please follow the link to GitHub shown above, then follow the links that mention orbital plotting, to see detailed descriptions and download options. The notebooks use volume data in the popular cube format.

______________________

Plotting rank-2 tensors

(explore on GitHub)
 
Image shows a gray wireframe representation of a finite capped segment of a carbon nanotube. Superimposed on the nanotube framework are two separate graphical representations of NMR carbon shielding tensors, one in the center of the tube and another one in one of the end caps. The principal axes of the tensors are shown with colored arrows centered on the relevant carbons, with green for positive shielding and red for negative shielding. The tensors are also represented by polar diagrams, with blue lobes for positive shielding and orange lobes for negative shielding. The images provide a 3D visualization of the NMR shielding tensors of the carbons, which would otherwise be represented by numerical data in a 3x3 matrix.
A Mathematica notebook for plotting graphical representations of NMR shielding tensors; easily adaptable for other types of rank-2 tensors (EFG, Optical Rotation, and others).
Description and some examples
Download the Mathematica (v. 12 and higher) notebook (60 kByte)
Here is the notebook for older Mathematica versions (up to v. 11) (52 kByte)
Download an XYZ molecular coordinate file read by the notebook (16 kByte)
If you use this plotting tool for your research, please cite the recommended references given at the top in the notebook.

______________________

Manipulate CUBE format volume data files

See the repository on on GitHub. manipulatecube is a Fortran tool used by me and my group to work with volume data files in the ’Gaussian cube’ format. You can use manipulatecube to multiply the volume data by a factor and integrate the cube, take linear combinations of two data sets (same grid, same molecule), add or multiply two cube files (same grid, same molecule), or use manipulatecube to bring a data set for an orthogonal but unsorted (not in the order x, y, z) grid, or a grid with negative steps (going from positive to negative coordinate values), into a more standard grid format. [Not all of the available visualization software packages can handle grids with negative steps or grids with vectors that aren’t in the order of x, y, z direction].

______________________

Crystal field Hamiltonian and atomic shell splitting

(explore on GitHub)
 
A plot is shown of the isotropic g-factor of the NpF6 molecule as a function of the ratio of crystal-field splitting Delta and the spin-orbit coupling constant zeta. The plot curve in blue rises across the plot from about -1.5 to over +1.0 on the vertical axis. The horizontal axis goes from zero to ten. An inset in the top left shows a 3D isosurface representation of one of the neptunium 5f atomic orbitals with orange and blue lobes. In the background of the image is a barely readable representation of the Hamiltonian matrix used to calculate the g-factor.
A Mathematica notebook for the symbolic calculation of a crystal field Hamiltonian and the spin-orbit coupling Hamiltonian in a basis of atomic orbitals for a given angular momentum ℓ, along with other calculations.
Description and some examples
Downloads the Mathematica notebook (792 kBytes)

______________________

PNMRShift: A software tool for NMR shifts of paramagnetic molecules

(explore on GitHub)
 
Graphics with a row of three separate xy plots showing NMR shielding tensor contributions as a function of reciprocal temperature. The line graphs are shown as examples for the kind of data that can be generated with the pNMRShift program.
Here you can download the source code along with Linux and Windows (32 bit) binaries of a program that reads calculated magnetic resonance tensors (Ramsey shielding, EPR Zeeman and hyperfine coupling), and optionally zero-field splitting, and assembles chemical shift tensors for a given temperature and pseudo-spin. For details see Reference [224]
Download PNMRShift (4.2 MByte. GPL)

______________________

KK-GUI: Software with graphical interface to perform Kramers-Kronig transformations

(explore on GitHub)
 
This software is useful if you have absorptive or dispersive spectral data and want to perform a Kramers-Kronig (KK) transformation to obtain the dispersive / absorptive counterpart. Works under Linux and Windows and comes in two versions that are both included in the package. Both versions are written in Python and use the Python interface with Tcl/Tk and Matplotlib for the GUI and the resulting plots. One version includes numerical routines in Fortran that need to be compiled. The second version is Python-only and does not require a compiler, but its KK transformations are slower. It is possible to perform ‘anchored’ KK transformations known as multiply subtractive KK (MSKK) or chained doubly-subtractive KK (CDKK); these methods are described in Reference [92]. KK-GUI was developed in 2017 by Mr. Herbert Ludowieg, then an undergraduate research assistant in my group, based on prior developments by Mark Rudolph, Patrick Dawson, and Mikhail Krykunov.
Download KK-GUI (458 KByte. GPL)
Below is a screen shot of the interface. We loaded optical rotatory dispersion data (red curve) into the software and let it generate the corresponding circular dichroism spectrum (blue curve).
A screenshot of a software interface titled ’Kramers-Kronig Transformations’ showing data tables on the left and buttons such as ’Load Data’, ’Plot Input Data’, ’Execute KK Transform’, and settings options. Below the interface is a plotted graph window with spectral curves (red and blue) versus frequency units generated by the KK GUI software. There are buttons to show or hide the transformed data and to save the graph data to a file.

______________________

CD spectra toolkit

Note: Our spec-gen Python script provides much of the functionality of the old CD spectra toolkit, which is therefore no longer maintained.

Here you can download a package containing some Unix shell scripts and the Fortran source code for two programs. Compiled binaries for a 32 bit Linux system are included. The Fortran source code should compile with any f90 compiler. Please email me if it doesn’t.
Download gzipped tar archive (781 kByte)
Together the scripts and programs process the output of a time-dependent DFT CD spectrum calculation and generate a nice simulated spectrum. The CD spectrum can be calculated with ADF or with Turbomole. The parsers are easily adapted for other programs. Please see the included README file for instructions. You need gnuplot to generate the spectra. Here is an example from Reference [17]:
Two-dimensional plot of a calculated circular dichroism spectrum of a metal complex. The horizontal axis is the light wavelength in nanometer, going from approximately 200 to 700. The left vertical axis is the differential absorption coefficient for left vs. right circularly polarized light, in units of liter per mol and per centimeter ranging from -150 to +400. The spectrum is plotted in red and shows pronounced peaks and troughs. The calculated rotatory strengths are shown in the same plot as vertical ’sticks’ but without units.
Simulated CD spectrum of [Co(en)3](3+)

______________________

Template for plots of spectra (or other stuff) with Gnuplot and LaTeX

Here is a collection of scripts and instructions (tar format, 172K) to create plots of spectral data or similar types of scientific plots with Gnuplot and LaTeX. A description is provided here. Below is an example of the type of plots one can make with this script collection.

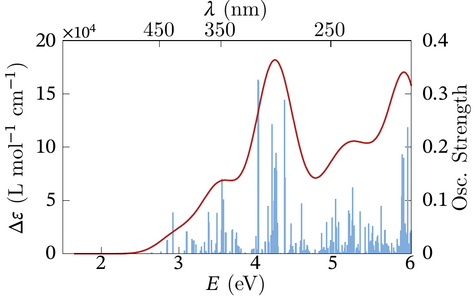
Two-dimensional plot of a calculated absorption spectrum of an unspecified molecule. The bottom horizontal axis is the photon energy in electron volts, going from approximately 1 to 6. The left vertical axis is the absorption coefficient in units of liter per mol and per centimeter, ranging from zero to 20,000. The spectrum is plotted in red and shows pronounced peaks. The calculated oscillator strengths are shown in the same plot as vertical blue ’sticks’ on a right vertical scale ranging from 0 to 0.4. A secondary horizontal axis at the top shows selected photon wavelengths corresponding to the energies at the bottom horizontal scale.

The CD spectra toolkit contains Gnuplot scripts with similar functionality, but they were not designed to be used with the epslatex terminal of Gnuplot. The latter was used to generate the plot above.

______________________

© 2013 – 2025 J. Autschbach. Some of the material that can be downloaded on this web page and the associated GitHub repository is in parts or wholly based on the results of research funded by grants from the National Science Foundation [NSF, grants CHE 0447321, 0952253, 1265833, 1560881, 1855470, 2152633, 2503332], the US Department of Energy (Basic Energy Sciences, Heavy Element Chemistry program, grant DE-SC0001136), and educational activities associated with these projects. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of these funding agencies.