Crystal field Hamiltonian and atomic shell splitting

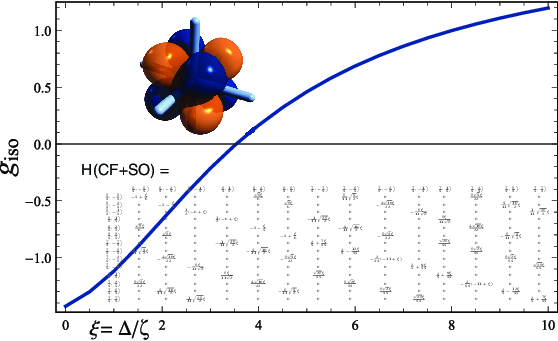
In publications [287], [216], and [211], among others, in collaboration with Dr. Hélène Bolvin, we used the crystal field (CF) splitting of atomic 4f and 5f orbitals in order to set up simple one-electron models to explain the observed magnetism of f${}^1$ complexes. During the time when I got involved in this research, I programmed the calculation of the simultaneous eigenfunctions of the CF and the spin-orbit (SO) Hamiltonian for a set of atomic orbitals with a given angular quantum number $\ell$ in Mathematica, essentially to learn how this stuff works.

You can download an example Mathematica notebook (792 kBytes) here. (See also our Downloads page). In there is a calculation for a $D_{4h}$ symmetric crystal field, for example to represent the ligand environment of the metal in a complex such as [NpO${}_2$Cl${}_4$]${}^{2-}$.

The calculation is done by setting up a basis of $|\ell ,m_{\ell },m_s⟩$ spin functions for an atomic shell with a given value of $\ell$. The CF is then represented by actual point charges, or by symbolic values, transformed to a representation in terms of spherical harmonics, and the operator matrix is calculated in the $|\ell ,m_{\ell },m_s⟩$ basis. We also calculate the SO operator

in the same basis and determine the ${Ĥ}^{\text{SO}}$ eigenfunctions $|j,m_j⟩$ in the basis $|\ell ,m_{\ell },m_s⟩$. Here, $\zeta$ is an empirical SO coupling constant. We then determine the eigenfunctions of the model Hamiltonian

in the $|\ell ,m_{\ell },m_s⟩$ basis as well as in the basis $|j,m_j⟩$ of the eigenfunctions of $H^{\text{SO}}$ (i.e. the atomic spinors). The eigenvalues of the model Hamiltonian can be plotted for different values of the CF parameters and $\zeta$.

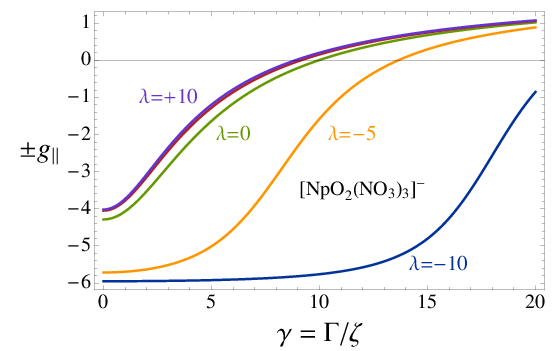
From the eigenvectors of ${Ĥ}^{\text{m}}$ and the matrix elements of the spin and angular momentum operators one can also generate information such as the electron magnetic moment (or rather the $g$ factor) for a magnetic field oriented in different directions relative to the molecule. The graphics at the top of this page are based on Mathematica calculations with notebooks similar to the one provided here, showing the electron $g$-factor of 5f${}^1$ actinide complexes for different ratios of selected CF parameters and the SO coupling constant. Details, and explanations of the notation, are provided in publications [286], [215], and [210].

© 2018 – 2024 J. Autschbach. The material shown on this web page is based on the results of research funded by a grant from the US Department of Energy (Basic Energy Sciences, Heavy Element Chemistry program, grant DE-SC0001136). Any opinions, findings, and conclusions or recommendations expressed here are those of the author and do not necessarily reflect the views of this funding agency.