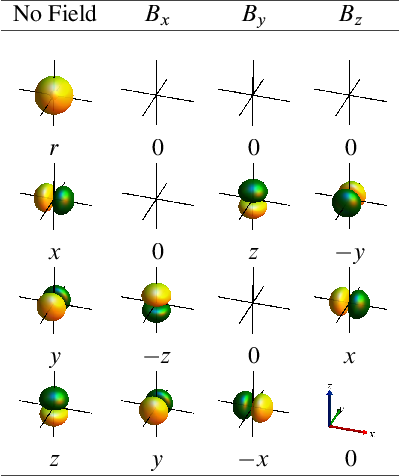
 orbitals:
orbitals: orbitals:
orbitals:
The sign and magnitude of magnetic properties such as NMR parameters can sometimes be rationalized with the help of ‘orbital rotation’ models. For an example, see this page explaining the substituent effects on the carbon NMR shifts in substituted benzenes. The idea behind such models is the following: An occupied orbital may contribute to the field-induced magnetic moment in a molecule if the action of the quantum mechanical magnetic field (‘B-field’) operator on the orbital results in a function that can overlap well with another unoccupied orbital in the molecule.
This statement has its origin in terms that appear in the NMR shielding tensor expression, for example, when written in a molecular orbital theory framework [1]:
|
| (1) |
The integral measures the overlap between an unoccupied molecular orbital (MO) and the function that is obtained from acting with the B-field operator on an occupied MO. The quantum mechanical B-field operator is proportional to the angular momentum operator and has three vector components, for the , , and direction. In simple models, one considers a representation of the molecular orbital in a minimal basis of so-called atomic orbitals (AOs).
Because of the relation to the angular momentum operator, the action of the B-field on an AO typically resembles a rotation of the AO. Below are Tables with worked-out results for , , , and orbitals, for magnetic fields in , , and direction. A factor of has been omitted from the magnetic field operator.
and
orbitals:
 orbitals:
orbitals:
 orbitals:
orbitals:

Orbital rotation models for orbitals have been in use in organic chemistry for quite some time to help rationalize trends in observed NMR chemical shifts [2, 3]. We have developed orbital rotation models for metal complexes with occupied and orbitals [4, 5]. For instance, by considering how the action of a magnetic field on the nonbonding orbitals in Pt(II) and Pt(IV) complexes results in an effective magnetic coupling with unoccupied metal-ligand orbitals rationalizes the large chemical shift difference between Pt chemical shifts for the two oxidation states [4].
[1] Autschbach, J. The calculation of NMR parameters in transition metal complexes. In Principles and Applications of Density Functional Theory in Inorganic Chemistry I, Vol. 112; Kaltsoyannis, N.; McGrady, J. E., Eds.; Springer: Heidelberg, 2004.
[2] Grutzner, J. B. Chemical shift theory. Orbital symmetry and charge effects on chemical shifts. In Recent advances in organic NMR spectroscopy; Norell Press: Landisville, NJ, 1987.
[3] Wiberg, K. B.; Hammer, J. D.; Zilm, K. W.; Cheeseman, J. R. J. Org. Chem. 1999, 64, 6394-6400.
[4] Autschbach, J.; Zheng, S. Magn. Reson. Chem. 2008, 46, S48-S55.
[5] Moncho, S.; Autschbach, J. Magn. Reson. Chem. 2010, 48, S76-85.
© 2011 – 2025 J. Autschbach. The material shown on this web page is in parts based on the results of research funded by grants from the National Science Foundation [NSF, grants CHE 0447321, 0952253, 1265833] and educational projects supported by these grants. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.